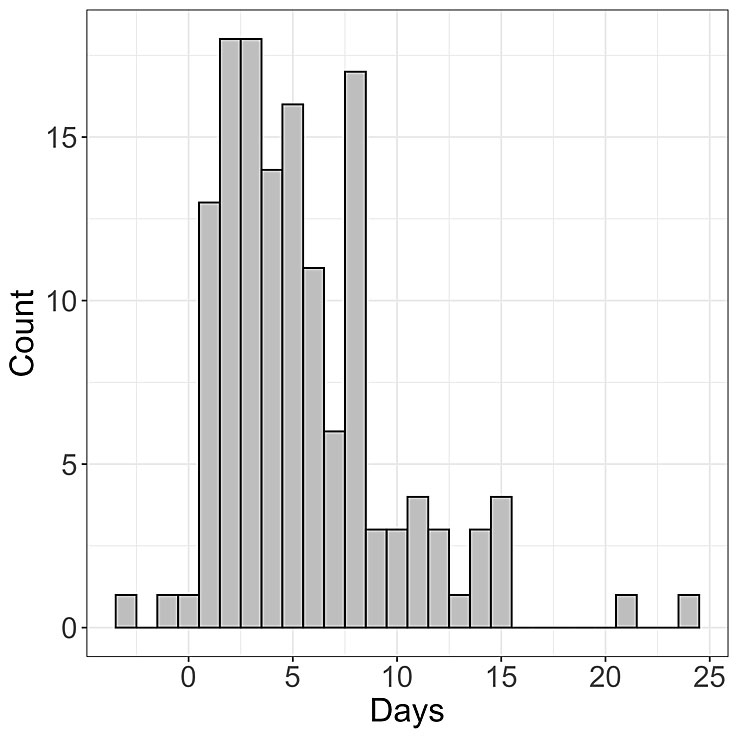
Figure 1 Time between COVID-19 symptom onset and case confirmation. Histogram of the time between symptom onset and case confirmation for 139 patients from Basel-Landschaft.
DOI: https://doi.org/10.4414/smw.2020.20271
The SARS-CoV-2 virus was first identified in China in December 2019 [1]. Switzerland recorded its first case on 25 February 2020. As of 22 April 2020, there were 28,154, 933 and 811 [2] documented cases in Switzerland, Basel-Stadt, and Basel-Landschaft, respectively. Initial COVID-19 cases had travel links to Italy [3, 4], indicating an import of infections from other locations. These imports seeded the initial COVID-19 epidemic in Switzerland. The subsequent rapid increase in the number of newly confirmed cases through time [5] reveals that infection then occurred mainly through so-called community transmission, i.e., transmission within Switzerland.
The reproductive number [6] quantifies the expected number of secondary infections caused by a single infected individual. In particular, the basic reproductive number quantifies the number of secondary infections in a completely susceptible population, and the effective reproductive number quantifies the number of secondary infections at a particular time-point of an epidemic. The basic reproductive number for COVID-19 has been estimated to be between 2 and 3.5 for China based on the initial number of confirmed cases through time. For an overview of papers estimating the basic reproductive number, see Liu et al. [7]. Estimating the basic reproductive number based on confirmed cases in locations different from China is not straightforward because early dynamics were driven by imports seeding the epidemic outbreaks. Using genomic sequences of SARS-CoV-2, we confirmed the basic reproductive number to be between 2 and 3.5 for China, as well as for Italy and Washington State (USA) [8]. Several groups (e.g., [9–11]) report the effective reproductive number for different countries and regions.
Here, we aimed at quantifying the effective reproductive number for the epidemic in Switzerland and in 10 of the 26 cantons forming the Swiss Confederation. The cantons for which we present analyses are among those most affected by COVID-19, as measured by absolute case numbers. We further performed sensitivity analyses for the epidemic in Switzerland and the epidemics in the Cantons of Basel-Stadt and Basel-Landschaft. Hereafter, we refer to the effective reproductive number as the reproductive number or as R(t), with t denoting the time point for which we determine the reproductive number. We will update estimates for R(t) as the epidemic unfolds in the future.
We used data from COVID-19 cases in Basel-Landschaft to estimate the infection time of the disease. We obtained line list information for 166 patients from the Cantonal Office of Public Health, Economics and Health Directorate of Basel-Landschaft. The time of symptom onset and case confirmation for 139 patients and the time of symptom onset and hospitalisation for 112 patients was extracted. We summarised these data by calculating the mean and standard deviation of the time between symptom onset and confirmation and the time between symptom onset and hospitalisation.
We estimated R(t) based on three different datasets. We obtained the cumulative number of confirmed COVID-19 cases over time for Switzerland and for the Swiss cantons and the cumulative number of deaths over time for Switzerland from the Specialist Unit for Open Government Data of the Canton of Zurich [2]. We retrieved these data via an online data repository [5] and accessed all data up to and including 22 April 2020.
We additionally obtained the total number of new COVID-19 cases admitted to the hospital per day for the University Hospital Basel (USB) in Basel-Stadt. This number is smaller than the total number of hospitalisations in Basel-Stadt as other hospitals also admit COVID-19 patients. Further, we obtained the number of new COVID-19 cases admitted to the hospital per day for the Bruderholzspital in Basel-Landschaft with the patients being Basel-Landschaft residents. This number represents the total hospitalisations within the canton among residents of the canton since the Bruderholzspital is the only hospital in Basel-Landschaft admitting COVID-19 patients. This hospitalisation data is available up to 31 March 2020.
Finally, up to 31 March 2020, we obtained the absolute number of tests performed per day and the number of positive tests per day from the two testing centres predominantly performing tests in Basel-Landschaft (Münchenstein and Lausen; open since 18 March 2020 [12]), as well as from the University Hospital in Basel-Stadt (in particular, all the samples from a major cantonal testing centre, which has been open in its current form since 9 March 2020 [13], are processed in the hospital, together with further samples).
We estimated the reproductive number R(t) as a function of time based on the number of confirmed cases per day. As sensitivity analyses, we additionally estimated R(t) based on the number of deaths per day for Switzerland and the number of new hospitalisations per day for the Basel-Landschaft and Basel-Stadt cantons.
R(t) is the expected number of secondary cases caused by an infected individual at a time point t. R(t) was estimated employing the method from [14] using the implementation in the R package EpiEstim on CRAN [15]. It is assumed that an individual who has had a COVID-19 infection for s days has an infection intensity ws . Let the number of newly infected individuals on day t-s be I(t-s). Then the expected number of newly infected individuals at time t is:
To estimate the posterior probability distribution of R(t), the full probability distribution for I(t) was considered (see Web Appendix 1 in [14]). We used the default prior for R(t) in EpiEstim (mean 5, standard deviation 5).
We do not know I(t), but we can measure quantities that are closely related to I(t). Here we first used the number of confirmed cases as a proxy. Second, we used the number of newly admitted COVID-19 patients to a hospital as a proxy. Third, we used the number of deaths as a proxy. Since a case confirmation, a hospitalisation, and a death event happen some days after the infection of the patient, for each such event, we needed to estimate the corresponding infection time in order to have a proxy that is directly proportional to I(t). Thus, for each observed patient (observed through case confirmation, hospitalisation, or death), we simulated their infection time. This is similar to what was also proposed by Abbott et al. [9, 16].
To simulate this infection time, we first assumed an incubation period, which is gamma-distributed with a mean of 5.3 days (standard deviation 3.2 [17]). After the incubation period, symptoms appear. We again assumed a gamma distribution for the time between symptom onset and the observed event (with an event being case confirmation, hospitalisation or death). The mean time between symptom onset and case confirmation was estimated from our Basel-Landschaft data (see “Results”) to be 5.6 days (standard deviation 4.2). The mean time between symptom onset and hospitalisation was estimated to be 6.6 days (standard deviation 4.6; see “Results”). The gamma distribution for the time between symptom onset and death was assumed to have a mean of 15 days (standard deviation 6.9 [17]).
For each confirmation, hospitalisation or death event, we sampled first from the incubation period distribution and then from the distribution of the time interval between symptom onset and the event. We subtracted the simulated infection time from the event time to obtain a proxy for the time of infection. This was done 100 times, meaning we obtained 100 time series of infection times.
So far, the simulated time series represent estimated infection times for confirmed patients. However, the number of simulated infections at time s days ago may be missing some individuals whose cases have not yet been confirmed but will be confirmed later. Let ps be the probability of an infection event having been confirmed after s days (given the infection will be confirmed eventually). We estimated ps by simulating waiting times between infection and case confirmation using the same distributions as for the incubation period and the time between symptom onset and confirmation as above. ps is taken to be the fraction of simulated infections confirmed within the first s days of infection. Finally, we used our estimates of ps to correct the time series: the number of infections at s days prior to the last day for which we have data was approximated by (number of simulated infections at s days prior to today)/ps. This corrected time series was used for estimating R(t).
For the distribution of ws , we used the serial interval estimated for COVID-19 infections from [18], with a mean of 4.8 days and a standard deviation of 2.3. Based on this assumption, >90% of onward transmissions happen within 8 days after infection of an individual.
We calculated a posterior distribution for R(t) using the Bayesian methodology provided in [15], based on each of the 100 time series of infection events obtained above. To reduce the influence of stochastic outliers, we smoothed the resulting R(t). The smoothed R(t) is calculated based on assessment of the number of new infections at times t, t-1 and t-2 (i.e., for a 3-day window assuming R is constant during that time; see equation above and [15]).
We reported the median of the mean R(t) estimates from the 100 infection time series. Second, we reported the median of the first and last 40-quantile of the posterior distribution for the uncertainty interval (key uncertainty interval approximating the 95% uncertainty interval). Third, we reported the first 40-quantile of the 100 obtained first 40-quantiles, and the last 40-quantile of the 100 obtained last 40-quantiles (wide uncertainty interval approximating a 95% uncertainty interval for the bounds of the key uncertainty interval).
When estimating R(t) from confirmation data, we relied on the testing intensity not changing through time [14]. On 6 March 2020, it was announced that the national strategy to fight COVID-19 changed from finding all COVID-19 positive cases and contact tracing to protecting the population at risk. This policy amounted to not testing every individual with symptoms. The alternative testing strategy was fully implemented starting 9 March 2020, but was subsequently reversed on 22 April 2020. After that date, testing of all individuals with symptoms resumed [19].
More than 90% of individuals transmit within 8 days, based on our serial interval assumption. Thus, we can estimate R using comparable testing data from 17 March onwards (9 March + 8 days). Since we have a reporting delay of about 10 days, this corresponds to R(t) estimates from 7 March onwards. Based on confirmation data up to 22 April we can estimate R(t) only until 12 April because of the reporting delay. We therefore show R(t) estimates from 7 March 7 to 12 April for the confirmation data.
In summary, we show R(t) estimates for the time period when Switzerland did not test all symptomatic patients. In our daily updates for the reproductive number provided on our webpage [20], the R(t) for 13 April until at least 20 April may be overestimated owing to the change in testing regimen. Thus, we will also show results based on hospitalisation data on our website in order to obtain robust estimates for 13–20 April 2020.
In addition to the sensitivity analyses regarding the data set mentioned above (i.e., analyses based on cases, hospitalisations, and deaths), we performed a separate analysis assessing the sensitivity of the results to the statistical method. Specifically, we estimated the case reproductive number Rc(t). Rc(t) is defined as the expected number of individuals that an individual becoming infected at time t causes over the period of its infection [21]. Thus, Rc(t) takes into account future events. In contrast, R(t) is based on past events; it was defined as the number of secondary infections caused by the individuals who transmit at time t. As a consequence, when calculating Rc(t), a proxy for the number of infections after time t is needed. In fact, since individuals will transmit within 8 days of infection with >90% probability (based on our serial interval assumption), we require data on the number of infections on the interval [t, t + 8 days] in order to estimate Rc(t). We use the implementation within EpiEstim [15] for calculating Rc(t).
The mean time between symptom onset and a case being confirmed is estimated to be 5.6 days (standard deviation 4.2), see figure 1. Based on a mean incubation period of 5.3 days [22], a case is only confirmed around 10.9 days after infection. Thus we can only quantify the reproductive number R(t) up to about 10 days prior to today. The mean time between symptom onset and hospitalisation is estimated to be 6.6 days (standard deviation 4.6).

Figure 1 Time between COVID-19 symptom onset and case confirmation. Histogram of the time between symptom onset and case confirmation for 139 patients from Basel-Landschaft.
In figure 2A, we show the cumulative number of confirmed cases (line) and the daily number of new cases (bars) for Switzerland and 10 out of the 11 cantons with the most confirmed cases on 31 March 2020. Graubünden was among the 11 cantons with the most cases; however, we omitted it owing to lack of data.
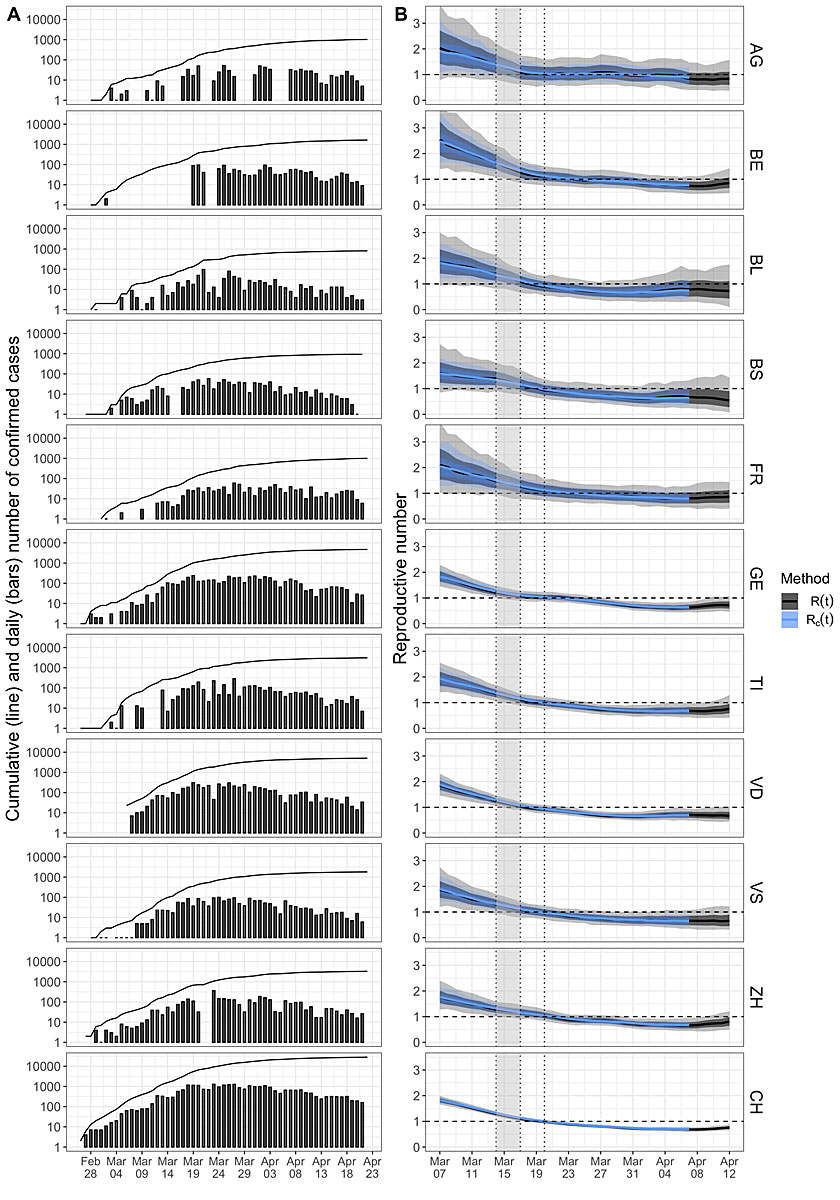
Figure 2 Reproductive number of COVID-19 in Switzerland and 10 cantons. A: The line shows the cumulative number of confirmed COVID-19 cases in Switzerland and 10 cantons. The bars show the number of newly confirmed cases for a particular day. Note that the y-axis is on a log scale. B: The reproductive number through time estimated based on the confirmed case data. In black, we show the median of means for R(t) and the lighter areas correspond to the two uncertainty intervals. In blue, we show the estimated values for Rc(t) as a sensitivity analysis. The vertical dotted lines are public health measures. In particular, the right of the gray interval is the time of the “Ausserordentliche Lage” (a lockdown) with non-essential shops and schools being closed. The dashed horizontal line highlights the threshold value R(t)=1.
In figure 2B, we show in black the R(t) through time based on the confirmed case data for 7 March 7 to 12 April. Values of R(t) >1 correspond to the exponential growth of the epidemic, whereas values of R(t) <1 imply exponential decline.
In order to compare the R(t) estimates through time with public health policies [23], we highlight changes in policies with dotted vertical lines and a gray area (figs 2 and 3 ). In particular, we display:
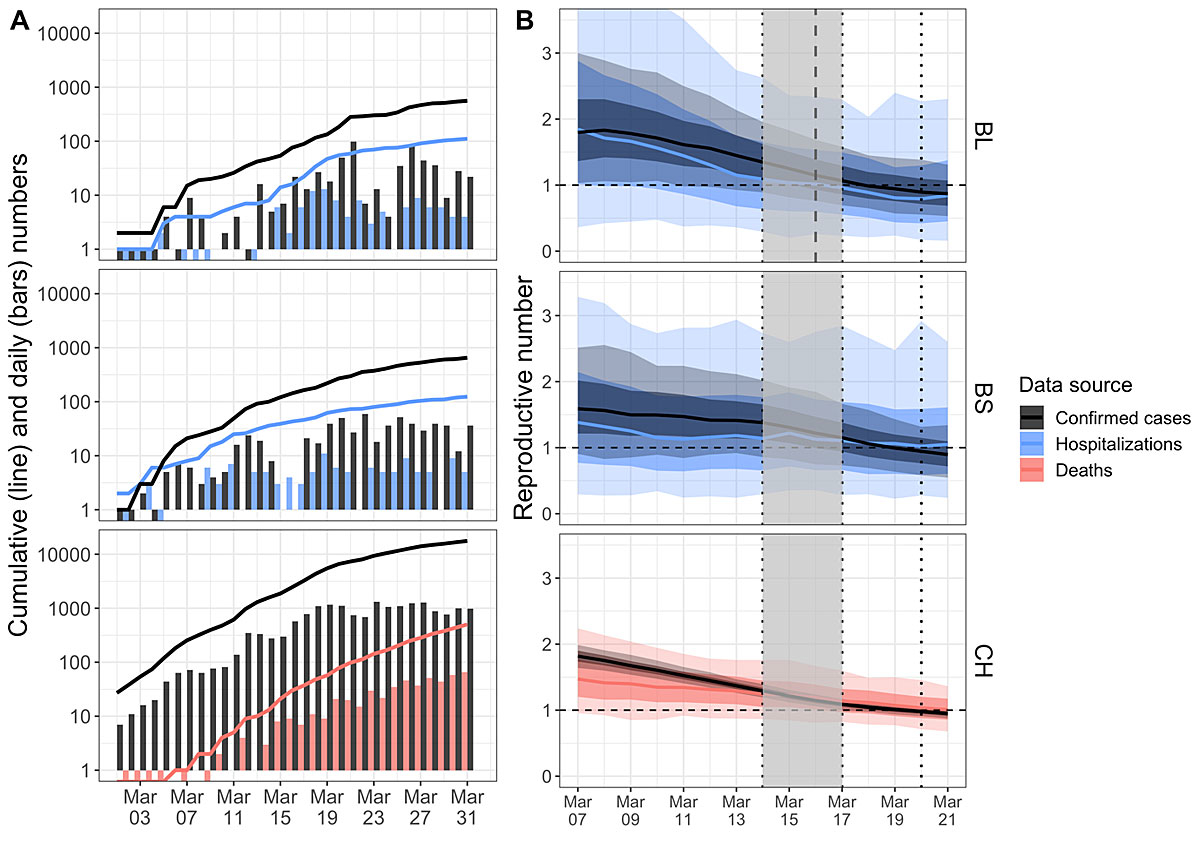
Figure 3 Reproductive number of COVID-19 in Switzerland and the Cantons Basel-Stadt and Basel-Landschaft including sensitivity analyses. A: The black line shows the cumulative number of confirmed COVID-19 cases in Switzerland as well as the Cantons of Basel-Stadt and Basel-Landschaft. The black bars show the number of newly confirmed cases for a particular day. The red line shows the cumulative number of deaths for Switzerland and the blue line shows the cumulative number of hospitalisations for the cantons. The bars again show the number of new deaths or hospitalisations for a particular day. Note that the y-axis is on a log scale (thus no bar means 1 case and a bar from 1 down means 0 cases).
B: The estimates for R(t) based on the confirmed case data for the Cantons of Basel-Landschaft (top, black), Basel-Stadt (middle, black), and Switzerland (bottom, black) and the estimates for R(t) based on the number of COVID-19 related hospitalisations in Basel-Landschaft (top, blue), at the University Hospital Basel-Stadt (middle, blue), and the number of COVID-19 related deaths in Switzerland (bottom, red). Again, the solid lines are the median of means and the lighter areas are the two uncertainty intervals. The R(t) values to the right of the dashed line for Basel-Landschaft are obtained based on confirmed data collected under the same testing policy (in the other two plots, testing policy did not change). The vertical dotted lines are public health measures. In particular, the right of the gray interval is the time of the “Ausserordentliche Lage” (a lockdown) with non-essential shops and schools being closed. The dashed horizontal line highlights the threshold value R(t)=1.
As described in the “Materials and methods” section, we performed a sensitivity analysis addressing the statistical method. The blue lines in figure 2B are the estimates of the case reproductive number Rc(t). We shifted this plot by 5 days compared with the R(t) plot: 4.8 days is the mean serial interval, which implies that, at any point in time t, new infections are driven by individuals infected on average 4.8 days before time t. Thus, by shifting Rc(t) by 5 days, the R and Rc curves should roughly align. Indeed, we observe the same patterns for R(t) and Rc(t-5) (see also [14]).
Overall, we observed a decline in R(t) in the first half of March. R(t) dropped below 1 after the most recent measure (5-people rule) was implemented on 20 March. R(t) has remained significantly below 1 since. Thus, since the last week of March, the epidemic has been under control (R(t) <1). However, our analysis does not allow us to draw conclusions about specific causes for the change in R(t). The dynamics in the cantons follow the same trend; however, the level of uncertainty is larger, as expected.
In figure 3 we show detailed results for Switzerland and the cantons of Basel-Stadt and Basel-Landschaft. We again show estimates for R from 7 March onwards, until the last date for which we have data on new hospitalisations in the cantons, 31 March 2020.
Again, we have highlighted implementations of public health policies as in figure 2. We note one additional measure for Basel-Stadt. As of 19 March, the criteria for self-isolation in Basel-Stadt became stricter: individuals with COVID-19 symptoms need to self-quarantine for at least 10 days (compared with 24 hours after last symptoms up to 19 March). People in the same household as a sick person need to self-quarantine for 10 days (compared with 5 days from 9 March 9 to 19 March). This intervention was implemented at almost the same time as the 5-people rule, so we only include the dotted line on 20 March.
In Basel-Stadt, the main testing centre opened on 9 March [13]. Their testing policy was not changed until 31 March. Thus our R(t) estimates should not be biased becuase of changes in testing from 7 March onwards (9 March + 8–10 days, see above). In Basel-Landschaft, the two testing centres predominantly performing tests in that canton opened on 18 March [12]. Their testing policies were not changed until 31 March, meaning we are confident in our R(t) estimates from 16 March onwards (dashed line).
The testing intensity between 9 and 31 March may have changed throughout the time course of this COVID-19 epidemic in Switzerland, despite official recommendations (including the policies of the testing centres in Basel-Stadt and Basel-Landschaft) not having changed until 31 March. For example, a decrease in testing through time due to a shortage of tests and swabs could, in principle, cause the observed decrease in estimated R(t) through time.
In order to address this potential confounding factor, for Switzerland, we compared the estimates of R(t) based on the number of confirmed cases through time to the R(t) based on the number of deaths due to COVID-19 through time. We argued that although the chance of a COVID-19 case being confirmed depends on the testing intensity at that time, the chance of death due to COVID-19 being reported does not change through time. Figure 3A (bottom) shows the number of confirmed cases and the number of deaths through time (cumulative: lines; per day: bars). Figure 3B (bottom) reveals that both data sources indicate the same trend; however, the estimates based on the death data are much more uncertain, which is expected as the deaths are a subset of the number of confirmed cases.
For the cantons of Basel-Stadt and Basel-Landschaft, we compared the number of confirmed cases through time and the number of newly hospitalised COVID-19 patients. Again, until 31 March there were no changes in the guidelines for when to hospitalise a patient. Thus we have no reason to suspect that the chance of a COVID-19 case being hospitalised changed through time. In Figure 3A (top and middle), we show the number of confirmed cases and the number of hospitalisations. Figure 3B (top and middle) shows the estimates of R(t).
For both cantons, the uncertainty intervals for the hospitalisation data are very wide because the number of hospitalisations are rather small. Basel-Landschaft estimates based on hospitalisations show the same trend in R(t) as the estimates based on confirmed cases. For Basel-Stadt, we obtained a very minor signal for a decrease in R(t) and have very wide uncertainty intervals, indicating that the data do not contain much information.
Finally, we looked at the ratio of the number of positive tests to the total number of tests per day for the University Hospital in Basel-Stadt (in particular, all the samples from the main cantonal testing centre which has been open in its current form since 9 March are tested at this hospital), and for the two testing centres in Basel-Landschaft (open since 18 March), see figure 4. The correlation between time and ratio was not significant for either canton (p-value for Basel-Stadt 0.21; for Basel-Landschaft 0.57). We want to highlight that these testing centres do not only test people from the respective canton. Further, some people from the respective canton may be tested elsewhere. Nevertheless, being the major testing centres of the cantons, the relative numbers should indicate the trend of testing intensity for the respective canton.
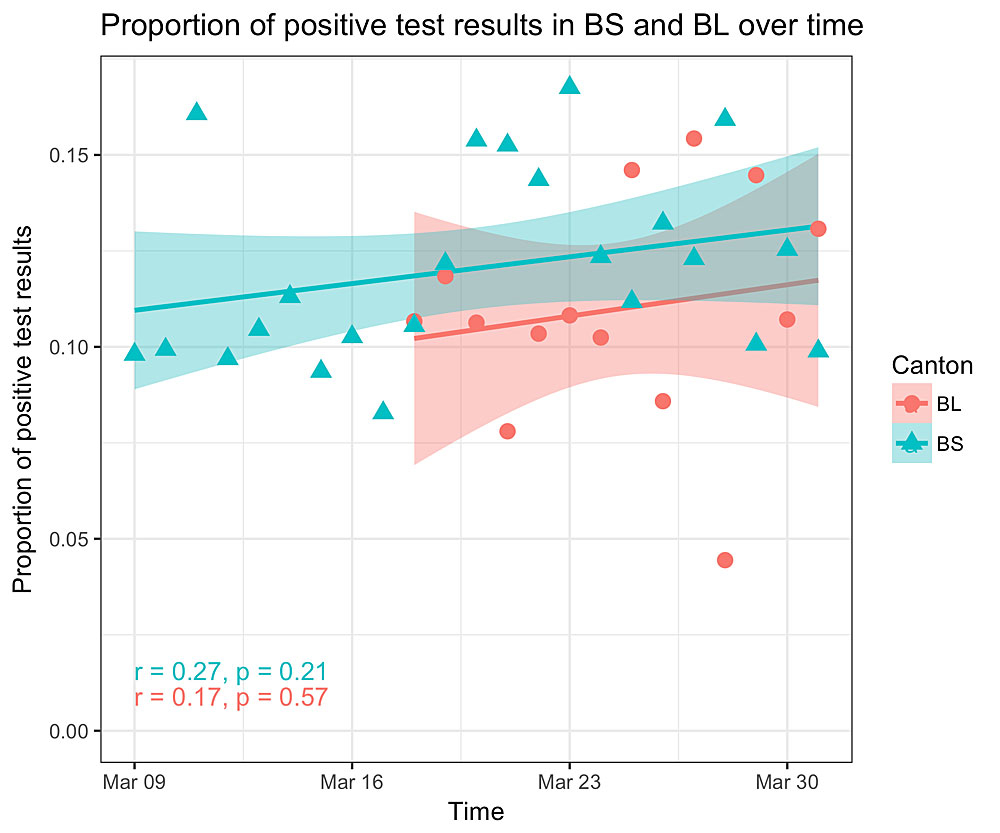
Figure 4 Proportion of COVID-19 positive tests per day in testing centers of Basel-Stadt (BS) and Basel-Landschaft (BL). We show the ratio of the number of positive tests and the number tests per day performed (i) at the University Hospital Basel-Stadt and (ii) the two testing centres in Basel-Landschaft. If testing intensity decreased since the testing centres opened, we would expect an increase in this ratio as we would expect a trend towards testing individuals with stronger symptoms. We plotted the regression line and the 95% confidence interval. However, the correlation between time and ratio is not significant.
Data on the spread of COVID-19 through time are of utmost importance to control this pandemic. An important measure obtained from the data is the reproductive number through time. Here, we investigated if changes in testing intensity could bias the reported reproductive number, and see no indication for major biases based on comparing confirmed case data and death data.
We saw a continuous decline of the reproductive number through time in the second and third weeks of March. From the last week of March onwards, the reproductive number was significantly below 1, which corresponds to a decline in the epidemic. A similar trend was estimated in [10, 16, 24] (accessed on April 24). Importantly, although we can look at the correlation between the reproductive number and public health measures, we cannot assess causation using our tools. Some approaches [11, 24] aim at identifying the causes of R(t) changes. In general, as the different measures were introduced very rapidly, it is hard to disentangle the effect of individual measures.
Nevertheless, monitoring of R(t) can help health officials to evaluate if the epidemic is under control. In response to indications of a growing epidemic (R(t) >1), officials could implement more protective measures in advance to prevent overload of hospital capacity. Conversely, in response to indications of a shrinking epidemic (R(t) <1) officials could carefully relax protective measures in combination with wide-spread testing, contact-tracing and isolation to avoid a rebound [25]. Important in this respect is that the reporting has a delay of about 10 days, as new infections are reported with a delay of about 10 days. This also holds for the related approach described in [16]. Only approaches making extra assumptions in order to extrapolate from the time interval covered by the data points can provide more recent predictions, see for example [26]. Such predictions are not made on a daily basis, though.
For estimating the R(t), we used the method presented in [14]. We see one main caveat when using this method. This method assumes that all infections are included in the analysis. However, in Switzerland, mainly individuals belonging to risk groups were tested for COVID-19 during the time period considered. If the proportion of unreported cases is constant, then in expectation, the underlying theory is still correct as the proportion cancels out from the equation given above. In [14], it is shown in a simulation study that the R(t) estimates are also robust to underreporting when the full probability distribution is considered.
At the start of the Swiss epidemic, new infections were imports from other locations rather than community transmissions [4]. The imports can lead to an overestimation of R at the start of the outbreak. Thus we refrain from interpreting the estimated R(t) values at the beginning of March 2020. Further, migration between cantons may bias the within-canton estimates. Future phylodynamic analyses may be able to refine the reproductive values for the early epidemic in Switzerland and the epidemics in the cantons, based on genomic sequencing data using the concept proposed in [8].
In conclusion, monitoring an epidemic through modelling is an essential contribution to guiding prevention measures for society as well as for hospitals. We will update R(t) in real-time throughout the course of the epidemic on our website [20]. In this way, we intend to provide up-to-date information on the transmission dynamics of SARS-CoV-2 in Switzerland and its cantons.
All code for performing the analyses and all data compiled for this study is available on https://github.com/jscire/Swiss_covid_Re.
We thank Anne Cori for her helpful guidance on using the EpiEstim package. We thank Nathanaël Hozé for helpful discussions related to the work presented here. Further, we thank Christian Althaus and an anonymous reviewer for very helpful comments. TS thanks ETH Zürich for funding.
No financial support and no other potential conflict of interest relevant to this article were reported.
1 Chen L , Liu W , Zhang Q , Xu K , Ye G , Wu W , et al. RNA based mNGS approach identifies a novel human coronavirus from two individual pneumonia cases in 2019 Wuhan outbreak. Emerg Microbes Infect. 2020;9(1):313–9. doi:.https://doi.org/10.1080/22221751.2020.1725399
2openZH/covid_19 [Internet]. Specialist Unit for Open Government Data Canton of Zurich; 2020 [cited 2020 Mar 30]. Available from: https://github.com/openZH/covid_19
3New Coronavirus 2019-nCoV: first confirmed case in Switzerland [Internet]. [cited 2020 Apr 27]. Available from: https://www.bag.admin.ch/bag/en/home/das-bag/aktuell/medienmitteilungen.msg-id-78233.html
4Federal Office of Public Health (BAG). New coronavirus Covid-19: three new confirmed cases in Switzerland [Internet]. [cited 2020 Apr 2]. Available from: https://www.bag.admin.ch/bag/en/home/das-bag/aktuell/medienmitteilungen.msg-id-78268.html
5corona-data.ch for Switzerland [Internet]. [cited 2020 Mar 30]. Available from: https://github.com/daenuprobst/covid19-cases-switzerland
6 Anderson RM , May RM . Population biology of infectious diseases: Part I. Nature. 1979;280(5721):361–7. doi:.https://doi.org/10.1038/280361a0
7 Liu Y , Gayle AA , Wilder-Smith A , Rocklöv J . The reproductive number of COVID-19 is higher compared to SARS coronavirus. J Travel Med. 2020;27(2):taaa021. doi:.https://doi.org/10.1093/jtm/taaa021
8Vaughan T, Nadeau S, Scire J, Stadler T. Phylodynamic Analyses of outbreaks in China, Italy, Washington State (USA), and the Diamond Princess [Internet]. Virological. 2020 [cited 2020 Mar 30]. Available from: http://virological.org/t/phylodynamic-analyses-of-outbreaks-in-china-italy-washington-state-usa-and-the-diamond-princess/439
9Abbott S, Hellewell J, Munday JD, Chun JY, Thompson RN, Bosse NI, et al. Temporal variation in transmission during the COVID-19 outbreak | CMMID Repository [Internet]. [cited 2020 Apr 7]. Available from: https://cmmid.github.io/topics/covid19/current-patterns-transmission/global-time-varying-transmission.html
10Lemaitre J, Perez-Saez J, Azman A, Rinaldo A, Fellay J. Switzerland COVID-19 Scenario Report [Internet]. Available from: https://jcblemai.github.io/
11Flaxman S, Mishra S, Unwin J, Coupland H, Mellan TA, Zhu H, et al. Report 13 Imperial College London - Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries [Internet]. Imperial College London. [cited 2020 Apr 3]. Available from: http://www.imperial.ac.uk/medicine/departments/school-public-health/infectious-disease-epidemiology/mrc-global-infectious-disease-analysis/covid-19/report-13-europe-npi-impact/
12Basel-Landschaft Media release. Notlage Basel-Landschaft [Internet]. [cited 2020 Apr 2]. Available from: https://www.baselland.ch/politik-und-behorden/regierungsrat/medienmitteilungen/regierungsrat-beschliesst-weitergehende-massnahmen-um-die-ausbreitung-des-coronavirus-einzudaemmen
13University Hospital Basel. COVID-19 Testing Center Predigerkirche [Internet]. Unispital Basel. [cited 2020 Apr 2]. Available from: https://www.unispital-basel.ch/patienten-besucher/notfall/coronavirus/
14 Cori A , Ferguson NM , Fraser C , Cauchemez S . A new framework and software to estimate time-varying reproduction numbers during epidemics. Am J Epidemiol. 2013;178(9):1505–12. doi:.https://doi.org/10.1093/aje/kwt133
15Cori A, Cauchemez S, Ferguson NM, Fraser C, Dahlqwist E, Demarsh PA, et al. EpiEstim: Estimate Time Varying Reproduction Numbers from Epidemic Curves [Internet]. 2019 [cited 2020 Mar 30]. Available from: https://CRAN.R-project.org/package=EpiEstim
16Abbott S, Hellewell J, Thompson RN, Bosse NI, Meakin S, Munday JD. Covid-19: Estimates for Switzerland [Internet]. Covid-19. [cited 2020 Apr 24]. Available from: https://epiforecasts.io/covid/posts/national/switzerland/
17 Linton NM , Kobayashi T , Yang Y , Hayashi K , Akhmetzhanov AR , Jung SM , et al. Incubation Period and Other Epidemiological Characteristics of 2019 Novel Coronavirus Infections with Right Truncation: A Statistical Analysis of Publicly Available Case Data. J Clin Med. 2020;9(2):538. doi:.https://doi.org/10.3390/jcm9020538
18 Nishiura H , Linton NM , Akhmetzhanov AR . Serial interval of novel coronavirus (COVID-19) infections. Int J Infect Dis. 2020;93:284–6. doi:.https://doi.org/10.1016/j.ijid.2020.02.060
19Neue Strategie - BAG empfiehlt viel mehr Corona-Tests [Internet]. Schweizer Radio und Fernsehen (SRF). 2020 [cited 2020 Apr 24]. Available from: https://www.srf.ch/news/schweiz/neue-strategie-bag-empfiehlt-viel-mehr-corona-tests
20Stadler T, Website Computational Evolution Group. ETH Zürich [Internet]. [cited 2020 Mar 31]. Available from: https://bsse.ethz.ch/cevo/research/sars-cov-2.html
21 Wallinga J , Teunis P . Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am J Epidemiol. 2004;160(6):509–16. doi:.https://doi.org/10.1093/aje/kwh255
22 Li Q , Guan X , Wu P , Wang X , Zhou L , Tong Y , et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N Engl J Med. 2020;382(13):1199–207. doi:.https://doi.org/10.1056/NEJMoa2001316
23Federal Office of Public Health (BAG). Media releases [Internet]. [cited 2020 Apr 2]. Available from: https://www.bag.admin.ch/bag/de/home/das-bag/aktuell/medienmitteilungen.html?dyn_startDate=01.01.2016
24Banholzer N, Weenen E van, Kratzwald B, Seeliger A, Tschernutter D, Bottrighi P, et al. Estimating the impact of non-pharmaceutical interventions on documented infections with COVID-19: A cross-country analysis. medRxiv. 2020 April 21;2020.04.16.20062141.
25Salathé M, Althaus CL, Neher R, Stringhini S, Hodcroft E, Fellay J, et al. COVID-19 epidemic in Switzerland: on the importance of testing, contact tracing and isolation. Swiss Med Wkly [Internet]. 2020 Mar 19 [cited 2020 Apr 6];150(1112). Available from: https://smw.ch/article/doi/smw.2020.20225
26Flaxman S, Mishra S, Unwin J, Coupland H, Mellan TA, Zhu H, et al. Report 13 Imperial College London - Real time update of the results for Switzerland [Internet]. Imperial College London. [cited 2020 Apr 3]. Available from: https://mrc-ide.github.io/covid19estimates/#/details/Switzerland
TS conceived the idea of the study. JS and TS designed and performed the analyses. SN and TV provided feedback on the analysis design. GB assisted in analyses. TS and JS interpreted the results. RM, LM, TG, TE, CQ, MS, STS, MB, RB, WK, KSR, CHN, SB, HHH, AE, RK, AW, CAM, MM, TB, AM designed the testing procedures in their cantons and provided data. SF, KNK, and JS provided data. TS wrote the first draft of the manuscript. All authors critically revised the manuscript and contributed to the final version.
No financial support and no other potential conflict of interest relevant to this article were reported.