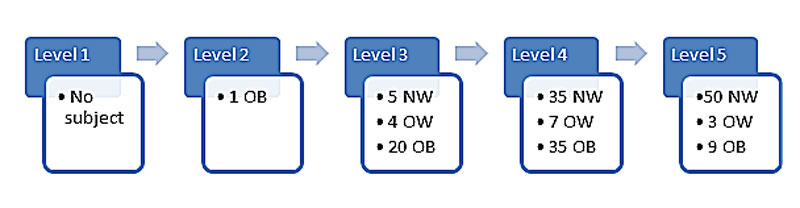
Figure 1 Characteristics of the subjects at each maximal intensity level reached.
NW = normal weight; OB = obese; OW = overweight
DOI: https://doi.org/10.4414/smw.2017.14435
The rapid increase in the prevalence of childhood obesity worldwide raises major concerns for global health [1]. Early diagnosis and management are essential to limit the development of comorbidities [2]. In children, treatment aims to limit weight gain during growth, and improve well-being and physical capacity, in order to prevent early comorbidities. One of the pillars of the treatment is engagement in regular physical activity [3], which has a beneficial effect on body composition as well as on cardiovascular disease risks [4]. Indeed, it is known that high cardiorespiratory fitness in youth is associated with a lower risk of myocardial infarction in later life [5]. It is important to be able to measure cardiorespiratory fitness in a clinical setting, not only to assess the risk of disease but also to evaluate the effects of physical activity programmes.
Maximal oxygen consumption (VO2max) is considered by the World Health Organization (WHO) to be the best cardiorespiratory fitness indicator [6] and is commonly assessed with treadmill or bike tests [7–9]. However, implementation of such tests has some limitations. First, they need expensive specialised equipment and expertise, limiting their use in clinical practice. Second, reference values are based on normal-weight populations and seem to underestimate the true VO2max in obese participants [10, 11]. These tests require maximal effort, which is often difficult to obtain from obese children. Indeed, based on our clinical practice, obese children experience rapid discomfort with signs of physical exhaustion within a few minutes. Consequently, maximal cardiorespiratory fitness tests are more difficult to perform in this population, which is why peak oxygen consumption is used. Therefore, a submaximal test, easy to perform and well tolerated by children, is needed. It is possible that a specific equation for predicting VO2 may also be needed for children because mechanical efficiencies may be different in children and adults [12].
It should be kept in mind that VO2max, expressed as an absolute value (e.g., in LO2.min-1), better represents the performance of non-weight-bearing activities such as cycling, swimming, handgrip force, etc. In this situation, obese individuals are less disadvantaged and sometimes perform better than control subjects [13]. However, obese individuals have more difficulties with daily activities like walking, sitting up/down and climbing stairs, because these activities are weight bearing. For this reason the VO2max, expressed as a relative value (e.g., in LO2.kg-1.min-1), better represents the ability of obese individuals to perform everyday tasks.
The Chester step test is a submaximal weight bearing test in which the subject has to step up onto and down from a bench (here 25 cm high) at an increasing pace to provide an estimate of peak oxygen consumption. A similar test was described in the 1960s by Margaria et al. [14], and was recently validated for adults [15]. Other studies have previously validated step tests in adults and children [16]. The Chester step test has the advantage of being easy to perform, is cheap and requires only a few light materials: a bench, a metronome and a device for heart rate measurement.
Finally, there is a need to assess whether earlier published VO2 predictions determined in adults [15, 16] are also applicable in children.
The aims of the study were to (1) elaborate an equation allowing the estimation of peak oxygen consumption using the Chester step test both in lean and obese children and adolescents and (2) compare these results with other prediction equations published in the literature.
This was a cross-sectional study including lean, overweight and obese children and adolescents aged 8 to 16 years. The tests were made not only for research purposes, but also to identify sedentary children at risk of cardiovascular diseases in order to initiate an activity programme. Obese participants were recruited at a paediatric obesity consultation at the secondary care public hospital of Sion (Wallis, Switzerland) between September 2009 and September 2012. Overweight and lean children with no regular physical activity (less than 5 hours per week including school activities, based on a physical activity questionnaire) were recruited at different schools located in Wallis during the same period. All participants came from the same demographic area (urban and rural) and were excluded from the study if they: (1) had an orthopaedic condition or a disease (e.g. cardiovascular disease) limiting physical activity; or (2) had a fracture or severe trauma of the lower limbs in the preceding year.
After they had been informed about the study, written consent was obtained from the parents and oral assent from the children. The protocol was approved by the ethics committee “Commission cantonale valaisanne d’éthique medicale ICHV” (no. CCVEM 037/09).
Body weight (kg) in light clothes and standing height (cm) were measured and body mass index (BMI) was calculated as weight / height squared (kg.m-2). The BMI z-scores were computed from the WHO references [17], to adjust BMI for age and gender. Overweight was defined as a BMI z-score between 1 and 2, and obesity as a BMI z-score greater than 2.
All participants had to climb up and down a 25 cm high step. This height was chosen to be optimal for the participants who might have had difficulties with the test (the youngest children of our study had a standing height of about 1.30 m) [18]. The rate was increased progressively from 15 to 35 cycles per minute with 5 cycles per minute increases [19]. According to the protocol, the test consisted of five stages, each lasting 2 minutes. Heart rate was recorded at the end of each stage using a heart rate sensor belt (Polar®). The oxygen consumption (VO2, ml.kg-1.min-1) was measured with a breath-by-breath analyzer Metamax (CORTEX Biophysik GmbH, Walter-Köhn-Str. 2d, 04356 Leipzig/Germany) throughout the test, and values for the last 30 seconds of each stage were kept for calculations. The participants were encouraged to continue until reaching criteria for maximal test: clinical signs of exhaustion or a heart rate higher than 85% of the theoretical age predicted maximum (220 minus age) and a respiratory quotient over 1.0 [8, 20]. We did not use the VO2 plateau as a criterion, as there is no such plateau in children [21].
The VO2peak (ml.kg-1.min-1) was also predicted using an available equation based on results in adults: the calculator for the Chester step test (ST calculator) (ASSIST creative resources Limited, Wrexham, Wales, http://the-chester-step-test-calculator.software.informer.com/6.0/) in which the maximal heart rate was defined as 220 minus age in years. This calculator predicts VO2peak using a linear extrapolation through the heart rate recorded at each intensity level and estimates VO2. The source of these VO2 values is not reported, but they depend only on the participants’ ages and the step height.
Both VO2 and heart rate were measured at each intensity level; thus participants had a maximum of five measurements. As some participants did not reach all levels, we dealt with missing values at highest levels as follows. Since the intensity increased at each level, both VO2 and heart rate were expected to increase accordingly; thus missing VO2 values would be at least as high as the last measurement and could then be considered as censored values. To deal with such data, we applied random-effects Tobit regression [22] using the “xttobit” command of Stata. The right-censoring variable was the highest measured VO2 for each participant, which was considered as the group variable. There were no missing data for the variables of interest.
The aim was to predict VO2 for each intensity level from age, gender and BMI z-score. We chose those variables because VO2 is known to be dependent on them [23]. Since 62 subjects achieved the fifth intensity level, the sample size was sufficient to include three covariates, with at least 15 observations per estimated parameter [24]. We first implemented separate models at each intensity level and noticed that the association between BMI z-score and VO2 increased with intensity, as did the difference between genders. The association with age remained constant through all levels. These observations suggested interactions between level and BMI z-score as well as between level and gender. As the increase in VO2 was almost constant across intensity levels, we considered this variable as continuous. Therefore, the VO2 was significantly predicted by age, gender, BMI z-score and intensity levels; including the above mentioned interactions – level × BMI z-score and level × gender.
It is not mandatory to have measurements for all five stages in order to estimate VO2peak. Nevertheless, the more levels obtained, the more precise the estimation can be.
Statistical differences between genders were analysed with the independent Student t-test. We used errors-in-variables regression [25] to compare the VO2peak values predicted by the proposed model and by the ST calculator. Linear regression was applied to assess the relationship between the predicted VO2peak values and the measured ones (for participants who reached criteria for maximal test as described above).
Differences were considered significant if p <0.05. Statistical analyses were performed using Stata 11.2 (StataCorp 2009, College Station, TX).
Reporting of this study follows the recommendations of the TRIPOD guidelines https://www.tripod-statement.org/.
The available data came from 169 children, whose characteristics are summarised in table 1. Mean (± standard deviation) age was 11.5 2.0 and mean BMI z-score was 1.2 ± 1.6. Forty-six percent of the subjects were boys, 53.3% were normal weight, 8.2% overweight and 38.5% obese. Both weight and height, but not age, increased with BMI z-score.
Table 1 Participants’ characteristics.
|
Boys
(n = 78) |
Girls
(n = 91) |
p-value
(t-test) |
Normal
(n = 90) |
Overweight
(n = 14) |
Obese
(n = 65) |
Total
(n = 169) |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | |
| Age (years) | 11.3 | (1.9) | 11.7 | (2.1) | 0.23 | 11.3 | (1.8) | 12.1 | (1.9) | 11.7 | (2.1) | 11.5 | (2.0) |
| Weight (kg) | 51.9 | (21.2) | 51.0 | (21.2) | 0.79 | 37.7 | (9.7) | 54.8 | (14.1) | 69.8 | (19.8) | 51.4 | (21.1) |
| Height (cm) | 150.2 | (13.0) | 149.4 | (12.6) | 0.70 | 147.0 | (12.5) | 153.3 | (12.6) | 152.9 | (12.3) | 149.8 | (12.7) |
| BMI z-score | 1.3 | (1.7) | 1.0 | (1.6) | 0.20 | -0.2 | (0.7) | 1.6 | (0.3) | 2.9 | (0.6) | 1.2 | (1.6) |
The children performed a Chester step test including a maximum of five intensity levels. One child did not reach the third level and stopped at stage two, 29 stopped at stage three, 77 at stage four and the 62 remaining children reached the fifth intensity level (fig.1).

Figure 1 Characteristics of the subjects at each maximal intensity level reached.
NW = normal weight; OB = obese; OW = overweight
Tobit models were applied to the VO2 measurements adjusted for age, gender, BMI z-score, and intensity level. BMI z-score and age were negatively associated with VO2, and girls had on average lower VO2 values than boys. The negative effect of BMI z-score on VO2 was stronger at higher intensity levels, and the gender difference was also greater at higher levels.
This model allows VO2 values to be estimated at each stage level using the following equation:
where gender = 0 for boys and 1 for girls, stage = 1 (i.e., 15 cycles per min), 2, 3, etc. BMI z score ranges from ˗3 to +3 and age is in years. VO2 is expressed in ml.kg˗1.min˗1. The confidence intervals for these coefficients are given in table 2.
Table 2 Coefficients of the Tobit model for VO2 prediction.
| Covariate | Coefficient | 95% Confidence interval | p-value |
|---|---|---|---|
| Intercept | 22.82 | 20.82, 24.82 | <0.001 |
| BMI z-score | ˗0.68 | ˗0.91, ˗0.44 | <0.001 |
| Age (years) | ˗0.46 | ˗0.63, ˗0.29 | <0.001 |
| Gender | ˗0.93 | ˗1.70, ˗0.15 | 0.019 |
| Stage | 4.07 | 3.94, 4.19 | <0.001 |
| BMI z-score * Stage | ˗0.24 | ˗0.29, ˗0.19 | <0.001 |
| Gender * Stage | ˗0.34 | ˗0.48, ˗0.19 | <0.001 |
Table 3 gives such VO2 values at each intensity level for different characteristics of the child (gender, age and BMI z-score). It allows the clinician to determine easily and very quickly the predicted VO2 of the subject, knowing the intensity level which was reached and the age and BMI z-score, without the need of the equation.
Table 3 Predicted VO2 values (mlO2.kg-1.min-1) according to gender, age, BMI z-score and intensity levels.
| Boys | Girls | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age | BMI z | Intensity level | Age | BMI z | Intensity level | ||||||||
| I | II | III | IV | V | I | II | III | IV | V | ||||
| 8 | ˗1 | 24.1 | 28.4 | 32.7 | 37 | 41.3 | 8 | ˗1 | 22.8 | 26.8 | 30.8 | 34.7 | 38.7 |
| 0 | 23.2 | 27.2 | 31.3 | 35.4 | 39.4 | 0 | 21.9 | 25.6 | 29.4 | 33.1 | 36.8 | ||
| 1 | 22.3 | 26.1 | 29.9 | 33.7 | 37.5 | 1 | 21 | 24.5 | 28 | 31.5 | 34.9 | ||
| 2 | 21.3 | 24.9 | 28.5 | 32.1 | 35.7 | 2 | 20.1 | 23.3 | 26.6 | 29.8 | 33.1 | ||
| 3 | 20.4 | 23.8 | 27.1 | 30.4 | 33.8 | 3 | 19.2 | 22.2 | 25.2 | 28.2 | 31.2 | ||
| 9 | ˗1 | 23.6 | 27.9 | 32.2 | 36.5 | 40.9 | 9 | ˗1 | 22.4 | 26.3 | 30.3 | 34.3 | 38.3 |
| 0 | 22.7 | 26.8 | 30.8 | 34.9 | 39 | 0 | 21.4 | 25.2 | 28.9 | 32.6 | 36.4 | ||
| 1 | 21.8 | 25.6 | 29.4 | 33.3 | 37.1 | 1 | 20.5 | 24 | 27.5 | 31 | 34.5 | ||
| 2 | 20.9 | 24.5 | 28 | 31.6 | 35.2 | 2 | 19.6 | 22.9 | 26.1 | 29.3 | 32.6 | ||
| 3 | 20 | 23.3 | 26.6 | 30 | 33.3 | 3 | 18.7 | 21.7 | 24.7 | 27.7 | 30.7 | ||
| 10 | ˗1 | 23.2 | 27.5 | 31.8 | 36.1 | 40.4 | 10 | ˗1 | 21.9 | 25.9 | 29.8 | 33.8 | 37.8 |
| 0 | 22.2 | 26.3 | 30.4 | 34.4 | 38.5 | 0 | 21 | 24.7 | 28.4 | 32.2 | 35.9 | ||
| 1 | 21.3 | 25.2 | 29 | 32.8 | 36.6 | 1 | 20.1 | 23.6 | 27 | 30.5 | 34 | ||
| 2 | 20.4 | 24 | 27.6 | 31.2 | 34.7 | 2 | 19.1 | 22.4 | 25.6 | 28.9 | 32.1 | ||
| 3 | 19.5 | 22.8 | 26.2 | 29.5 | 32.8 | 3 | 18.2 | 21.2 | 24.2 | 27.2 | 30.2 | ||
| 11 | ˗1 | 22.7 | 27 | 31.3 | 35.6 | 39.9 | 11 | ˗1 | 21.4 | 25.4 | 29.4 | 33.4 | 37.3 |
| 0 | 21.8 | 25.8 | 29.9 | 34 | 38 | 0 | 20.5 | 24.2 | 28 | 31.7 | 35.4 | ||
| 1 | 20.9 | 24.7 | 28.5 | 32.3 | 36.2 | 1 | 19.6 | 23.1 | 26.6 | 30.1 | 33.6 | ||
| 2 | 19.9 | 23.5 | 27.1 | 30.7 | 34.3 | 2 | 18.7 | 21.9 | 25.2 | 28.4 | 31.7 | ||
| 3 | 19 | 22.4 | 25.7 | 29 | 32.4 | 3 | 17.8 | 20.8 | 23.8 | 26.8 | 29.8 | ||
| 12 | ˗1 | 22.2 | 26.5 | 30.8 | 35.2 | 39.5 | 12 | ˗1 | 21 | 24.9 | 28.9 | 32.9 | 36.9 |
| 0 | 21.3 | 25.4 | 29.4 | 33.5 | 37.6 | 0 | 20.1 | 23.8 | 27.5 | 31.2 | 35 | ||
| 1 | 20.4 | 24.2 | 28 | 31.9 | 35.7 | 1 | 19.1 | 22.6 | 26.1 | 29.6 | 33.1 | ||
| 2 | 19.5 | 23.1 | 26.6 | 30.2 | 33.8 | 2 | 18.2 | 21.5 | 24.7 | 28 | 31.2 | ||
| 3 | 18.6 | 21.9 | 25.2 | 28.6 | 31.9 | 3 | 17.3 | 20.3 | 23.3 | 26.3 | 29.3 | ||
| 13 | ˗1 | 21.8 | 26.1 | 30.4 | 34.7 | 39 | 13 | ˗1 | 20.5 | 24.5 | 28.5 | 32.4 | 36.4 |
| 0 | 20.9 | 24.9 | 29 | 33 | 37.1 | 0 | 19.6 | 23.3 | 27.1 | 30.8 | 34.5 | ||
| 1 | 19.9 | 23.8 | 27.6 | 31.4 | 35.2 | 1 | 18.7 | 22.2 | 25.6 | 29.1 | 32.6 | ||
| 2 | 19 | 22.6 | 26.2 | 29.8 | 33.3 | 2 | 17.8 | 21 | 24.2 | 27.5 | 30.7 | ||
| 3 | 18.1 | 21.4 | 24.8 | 28.1 | 31.5 | 3 | 16.8 | 19.8 | 22.8 | 25.8 | 28.9 | ||
| 14 | ˗1 | 21.3 | 25.6 | 29.9 | 34.2 | 38.5 | 14 | ˗1 | 20 | 24 | 28 | 32 | 35.9 |
| 0 | 20.4 | 24.5 | 28.5 | 32.6 | 36.7 | 0 | 19.1 | 22.9 | 26.6 | 30.3 | 34 | ||
| 1 | 19.5 | 23.3 | 27.1 | 30.9 | 34.8 | 1 | 18.2 | 21.7 | 25.2 | 28.7 | 32.2 | ||
| 2 | 18.6 | 22.1 | 25.7 | 29.3 | 32.9 | 2 | 17.3 | 20.5 | 23.8 | 27 | 30.3 | ||
| 3 | 17.6 | 21 | 24.3 | 27.7 | 31 | 3 | 16.4 | 19.4 | 22.4 | 25.4 | 28.4 | ||
Furthermore, a good estimation of VO2max can be obtained by calculating the extrapolated VO2 at the heart rate maximum level, from the linear relationship between VO2 and heart rate [26]. The VO2peak value is predicted by performing a linear fit between the estimated VO2 at each level (as given in table 3) and the corresponding measured heart rate. The fitted value at the maximum heart rate (220 minus age) corresponds to the estimated VO2peak.
Figure 2 shows the associations between the measured VO2 values and those predicted by the ST calculator or by our proposed model. It highlights the wide dispersion of measured VO2 values at each intensity level, which is at odds with the fixed values suggested by the ST calculator, resulting in unreliable estimations of VO2peak. Our equation allows much more precise predictions which would improve the estimation of VO2peak.
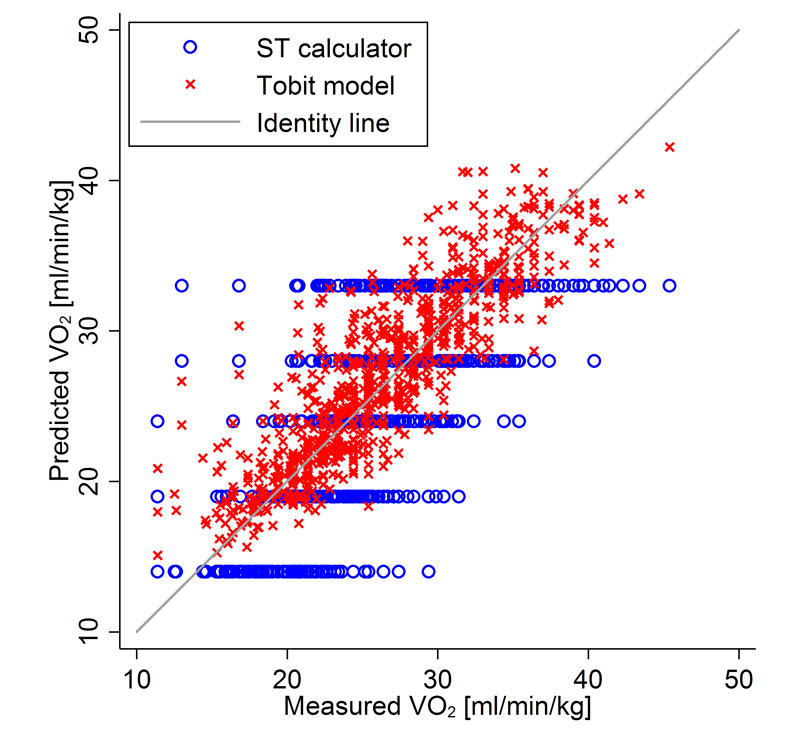
Figure 2 Comparison between the VO2peak values predicted by the ST calculator and the Tobit model.
The grey line represents the identity line, the red crosses represent the maximum oxygen consumption (VO2peak) predicted from our prediction equation (Tobit model) and the blue circles represent the VO2peak calculated from the Chester step test calculator.
Extrapolating our equation prediction to young adults with the same characteristics (male, 22 years and BMI z-score of 0) as those used by Buckley et al. [15], we found values similar to those they published for the ST calculator and given in Margaria et al. [14] (table 4).
Table 4 Comparison of VO2 values for each of the five intensity stages obtained by using different methods.
| Stage | I | II | III | IV | V |
|---|---|---|---|---|---|
| VO2 reported by Buckley | 14 | 19 | 24 | 28 | 33 |
| VO2 reported by Margaria | 16 | 20 | 24 | 28 | 32 |
| VO2 predicted from our equation |
16 | 20 | 24 | 28 | 32 |
VO2 expressed in mlO2.kg-1.min-1First row: VO2 predicted using the Chester step test calculator and reported from [8]. Second row: VO2 predicted by Margaria et al. [27] Third row: VO2 predicted extrapolated from the equation developed in the present study for adults with similar age (22 y), gender and BMI z score (0), as reported in [8].
In an attempt to verify the accuracy of the predicted VO2peak value provided by our model, we used the data of participants who reached a respiratory quotient of >1.0 and a heart rate higher than 85% of the maximum heart rate (n = 59). We then compared their highest measured VO2 value with the VO2peak predicted by our model and by the ST calculator. These predicted values are obtained using only the measurements of the first three intensity levels, as would be the case in a submaximal test (as performed in practice by clinicians). Figure 3 illustrates the associations between measured and predicted VO2peak. The confidence intervals (CIs) are computed from the standard error of the prediction; they show that the linear prediction is slightly more accurate with the Tobit model than with the ST calculator.
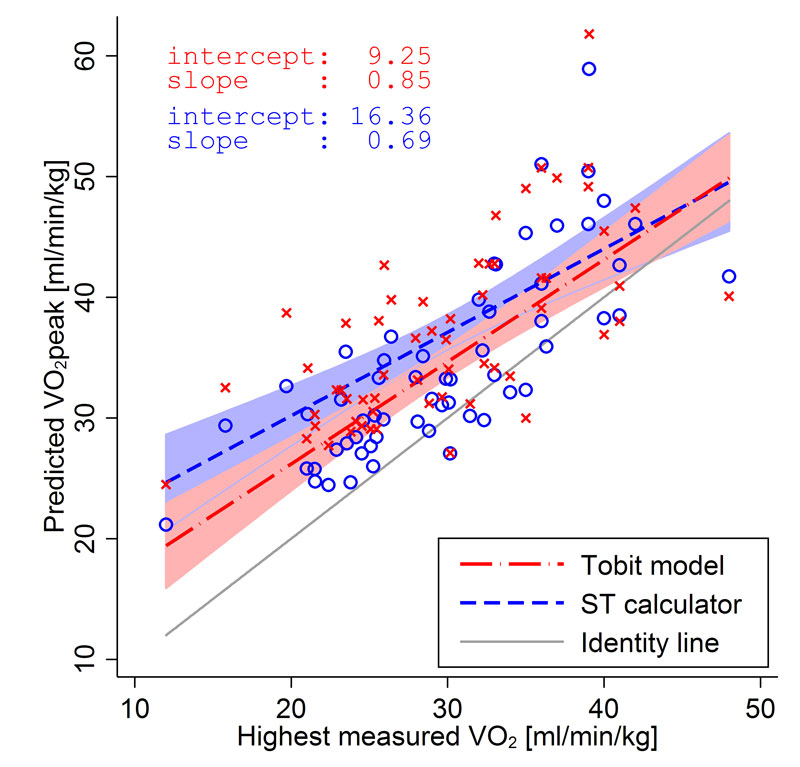
Figure 3 Comparison between the predicted maximum oxygen consumption (VO2peak) values and the highest measured VO2 in participants (n = 59) reaching criteria for maximal test.
Criteria for maximal test were: a respiratory quotient higher than 1.0 and a heart rate higher than 85% of the estimated maximal heart rate (220 ˗ age).
The predictions were obtained with the Tobit model (present study) (crosses and red line) or with an equation developed from data reported in the literature (ST calculator, open circles and dotted blue line), using the measurements of the first three intensity levels only (sub-maximal test). The grey line represents the identity line.
Using a linear regression model, we found a slope of 0.85 (95% CI 0.66–1.03) and an intercept of 9.25 (p = 0.002, 95% CI 3.66–14.84) for the Tobit model. This result suggests that there is an overestimation of predicted VO2peak but this is constant throughout all values (the slope is not significantly different from 1). With the VO2peak predicted by the ST calculator, the slope is 0.69 (95%CI 0.48–0.90) and the intercept 16.36 (p <0.001, 95%CI 10.02–22.69), which suggests that our model is more accurate. Moreover, the Pearson’s correlation between predicted VO2peak and the highest measured VO2 value is higher for the Tobit model (rho = 0.78, 95% CI 0.61–0.84) than for the ST calculator (rho = 0.66, 95% CI 0.46–0.76).
In this cross-sectional study, we developed an equation (by using an already validated step test) to predict VO2peak in a large panel of normal weight, overweight and obese children. In addition, we found that the oxygen consumption and the VO2peak determined in our study corresponded fairly to those published in the literature. Consequently, both aims of our study were achieved.
The continuous indirect calorimetric and heart rate measurements on a large sample of children and adolescents (a total of 169) during a step test protocol allowed us to construct a prediction equation of oxygen consumption at each exercise intensity (stage), if the gender, age and BMI z-score of the children are known. Based on the oxygen consumed and the heart rate at each exercise intensity, it was possible to determine, by extrapolation to the maximum heart rate (220 minus the age), the peak oxygen consumption of children with different ages and BMI z-scores. This estimate could be made with use of only a bench and a device to measure heart rate. In summary, our method estimates oxygen consumption at each stage level of a submaximal exercise and then predicts VO2peak by extrapolating the heart rate/ VO2 relationship to maximum heart rate.
Oxygen consumption: Our prediction equation for submaximal exercise confirmed earlier findings that boys have a higher oxygen consumption than girls [28–30]. This difference has been found throughout childhood or only during adolescence, depending on the study. Moreover, our study showed lower oxygen consumption per unit of body weight by obese participants during exercise than by their lean counterparts, suggesting a lower energy cost of this activity. This result is surprising, but compatible with some, but not all, results published in the literature in the field of human locomotion [31]. Further research is clearly needed in order to better understand this issue. Furthermore, when we used the equation developed in the present study to predict VO2 for young lean men (age 22 years, BMI z-score 0), we found results fairly similar to those of the ST calculator and Margaria et al. [14, 15] (see table 4).
Peak oxygen consumption: In accordance with the results published in the literature [29, 32, 33], we observed that VO2peak of obese children, expressed per unit of body weight, was lower than those of normal weight children.
It appears that the highest measured VO2 did not really reach the predicted VO2peak values (see fig. 3), even in the 59 children who fulfilled the maximal exercise criteria (85% of maximum heart rate and respiratory quotient over 1.0). These results may be due to a relative “low” maximal criteria limit, i.e., individuals who did not reach VO2peak were selected. It may also be possible that children (especially obese individuals) stopped exercising before reaching their maximal oxygen consumption as a result of coordination problems. On the other hand, some children may have reached their VO2peak but their predicted maximum heart rate was overestimated. This is supported by the findings of earlier studies that reported that “real” maximal heart rate was 7 (SD 8) to 10 (SD 8) beats per minute less than the predicted maximal heart rate (220 – age) [34, 35]. Thus, at least a fraction of the difference between both “real” and predicted maximal heart rate in our study i.e. 18 (SD 9) beats per minute (n = 59), may be explained by this “overestimation” of the predicted heart rate in children.
It appears that the prediction equation of our study slightly overestimates VO2peak, but the exact value of this small difference remains to be investigated more thoroughly. This can be explained by the fact that the highest value of VO2 determined with use of a “second criterion” (e.g. respiratory quotient) to assess whether VO2peak is reached, may probably underestimate VO2peak [20, 21, 36]. It must be kept in mind that our prediction equation of VO2peak takes into account age, BMI and gender, which certainly improve the accuracy of the results. Finally, we found a Pearson coefficient of 0.78 between the predicted VO2peak and the highest measured VO2, a coefficient which is within the range of those observed from equations prediction of VO2max from submaximal exercises found in adults, i.e., between 0.57 and 0.92 [37].
From our results we can say that the ST calculator should not be used in children for several reasons. First, we demonstrated that, in this population, the VO2 predicted by the calculator was not reliable, as there was a wide variation between subjects at each stage. Secondly, it takes into account neither gender, age, nor body composition, which have been shown to be associated with maximal oxygen consumption.
This study has several strengths and limitations. We explored a large number of children with wide ranges of and BMI and of both genders, allowing generalisation of our equation to a wide population. However, we performed neither test-retest for reproducibility of this test, which is nevertheless known to be reproducible [15, 16], nor a standard maximal test such as the bike or treadmill test. However, the step test is known to be reliable [16]. Furthermore, we did not evaluate the role of body composition (fat mass and lean body mass) in the evaluation of oxygen consumption and, consequently, its use in the equation. However, part of the difference in body composition variation has been addressed with the use of gender, age and BMI in the equation. Indeed, the BMI is easier and cheaper to obtain in clinical practice than body composition, and a good correlation has been found between the two [38]. Sexual maturation was not been evaluated in our study, but its influence on aerobic capacity remains controversial. For instance, some studies [27, 39], but not all [23], concluded that the increase in VO2peak during growth was mostly explained by changes in body composition/dimensions. Moreover, after adjustment for age, weight and height, the testosterone concentration was not related to VO2peak in boys [27]. In addition, the obese children were slightly taller than their normal counterparts of similar age, which confirms what is already known [40]. However, we do not think that this difference had an impact on our results, as height was included in the prediction equation. Finally, in our study, a maximal test, according to common criteria, could not be obtained from all participants, probably because of mechanical limitations at higher stages that necessitated good coordination. It underlines the fact that the step test was designed to be a submaximal test and that a maximal test is difficult to perform, especially in obese children.
We conclude that this study allowed the development of a valid equation to predict peak oxygen consumption during a submaximal Chester step test, in both lean and obese children. It underlines the necessity to take into account gender and BMI, in addition to age and intensity level, as girls and obese children have lower cardiorespiratory fitness.
We thank the participants for volunteering for the study, Patricia Pellissier (secretary) and the “Institut de Recherche en Réadaptation” for their assistance. Nathalie Farpour-Lambert is currently in the Obesity Prevention and Care Program “Contrepoids”, Service of Therapeutic Education for Chronic Diseases, Department of Community Medicine and Primary Care, University Hospitals of Geneva and University of Geneva, Switzerland
This study was supported financially by the “Délégation valaisanne de la Loterie Romande”, the “Commission de gestion du fonds cantonal de promotion de la santé” and the Geneva University Hospitals “Contrepoids” Research Funds. The work was independent of the funding.
The authors have no conflicts of interest to declare.
1 Lobstein T , Baur L , Uauy R ; IASO International Obesity TaskForce. Obesity in children and young people: a crisis in public health. Obes Rev. 2004;5(Suppl 1):4–104. https://doi.org/10.1111/j.1467-789X.2004.00133.x
2 Reilly JJ , Kelly J . Long-term impact of overweight and obesity in childhood and adolescence on morbidity and premature mortality in adulthood: systematic review. Int J Obes. 2011;35(7):891–8. https://doi.org/10.1038/ijo.2010.222
3 Waters E , de Silva-Sanigorski A , Hall BJ , Brown T , Campbell KJ , Gao Y , et al. Interventions for preventing obesity in children. Cochrane Database Syst Rev. 2011;12(12):CD001871.
4 Vasconcellos F , Seabra A , Katzmarzyk PT , Kraemer-Aguiar LG , Bouskela E , Farinatti P . Physical activity in overweight and obese adolescents: systematic review of the effects on physical fitness components and cardiovascular risk factors. Sports Med. 2014;44(8):1139–52. https://doi.org/10.1007/s40279-014-0193-7
5 Högström G , Nordström A , Nordström P . High aerobic fitness in late adolescence is associated with a reduced risk of myocardial infarction later in life: a nationwide cohort study in men. Eur Heart J. 2014;35(44):3133–40. https://doi.org/10.1093/eurheartj/eht527
6 Shephard RJ , Allen C , Benade AJ , Davies CT , Di Prampero PE , Hedman R , et al. The maximum oxygen intake. An international reference standard of cardiorespiratory fitness. Bull World Health Organ. 1968;38(5):757–64.
7 Cunningham DA , van Waterschoot BM , Paterson DH , Lefcoe M , Sangal SP . Reliability and reproducibility of maximal oxygen uptake measurement in children. Med Sci Sports. 1977;9(2):104–8.
8 Figueroa-Colon R , Hunter GR , Mayo MS , Aldridge RA , Goran MI , Weinsier RL . Reliability of treadmill measures and criteria to determine VO2max in prepubertal girls. Med Sci Sports Exerc. 2000;32(4):865–9. https://doi.org/10.1097/00005768-200004000-00021
9 Turley K , Rogers D , Harper K , Kujawa K , Wilmore J . Maximal Treadmill Versus Cycle Ergometry Testing in Children: Differences, Reliability, and Variability of Responses. Pediatr Exerc Sci. 1995;7(1):49–60. https://doi.org/10.1123/pes.7.1.49
10Bar-Or O. Physiologic Responses to Exercise of the Healthy Child. In: Pediatric sports medicin for the practioner. New York: Spring-Verlag, 1983, p. 1-65.
11 Krahenbuhl GS , Skinner JS , Kohrt WM . Developmental aspects of maximal aerobic power in children. Exerc Sport Sci Rev. 1985;13:503–38. https://doi.org/10.1249/00003677-198500130-00015
12 Villagra F , Cooke CB , McDonagh MJ . Metabolic cost and efficiency in two forms of squatting exercise in children and adults. Eur J Appl Physiol Occup Physiol. 1993;67(6):549–53. https://doi.org/10.1007/BF00241653
13 Esmaeilzadeh S , Ebadollahzadeh K . Physical fitness, physical activity and sedentary activities of 7 to 11 year old boys with different body mass indexes. Asian J Sports Med. 2012;3(2):105–12. https://doi.org/10.5812/asjsm.34709
14 Margaria R , Aghemo P , Rovelli E . Indirect determination of maximal O2 consumption in man. J Appl Physiol. 1965;20(5):1070–3.
15 Buckley JP , Sim J , Eston RG , Hession R , Fox R . Reliability and validity of measures taken during the Chester step test to predict aerobic power and to prescribe aerobic exercise. Br J Sports Med. 2004;38(2):197–205. https://doi.org/10.1136/bjsm.2003.005389
16 Watkins J . Step tests of cardiorespiratory fitness suitable for mass testing. Br J Sports Med. 1984;18(2):84–9. https://doi.org/10.1136/bjsm.18.2.84
17WHO Multicentre Growth Reference Study Group. WHO Child Growth Standards: Length/height-for-age, weight-for-age, weight-for-length, weight-for-height and body mass index-for-age: Methods and development. Geneva: World Health Organization; 2006. 312 pages.
18 Culpepper MI , Francis KT . An anatomical model to determine step height in step testing for estimating aerobic capacity. J Theor Biol. 1987;129(1):1–8. https://doi.org/10.1016/S0022-5193(87)80199-6
19 Sykes K . Capacity assessment in the workplace: a new step test. Occup Health (Lond). 1995;47(1):20–2.
20 Barker AR , Williams CA , Jones AM , Armstrong N . Establishing maximal oxygen uptake in young people during a ramp cycle test to exhaustion. Br J Sports Med. 2011;45(6):498–503. https://doi.org/10.1136/bjsm.2009.063180
21 Day JR , Rossiter HB , Coats EM , Skasick A , Whipp BJ . The maximally attainable VO2 during exercise in humans: the peak vs. maximum issue. J Appl Physiol (1985). 2003;95(5):1901–7. https://doi.org/10.1152/japplphysiol.00024.2003
22 Tobin J . Estimation of relationships for limited dependent variables. Econometrica. 1958;26(1):24–36. https://doi.org/10.2307/1907382
23 Armstrong N , Welsman JR . Peak oxygen uptake in relation to growth and maturation in 11- to 17-year-old humans. Eur J Appl Physiol. 2001;85(6):546–51. https://doi.org/10.1007/s004210100485
24Harrell F. Regression modeling strategies: with applications to linear models, logistic and ordinal regression, and survival analysis. New York: Springer; 2015.
25Carroll RJ, Ruppert D, Stefanski LA. Regression Calibration. In: Measurement Error in Nonlinear Models, edited by Hall C. New York: 1995, p. Chapter 4.
26 Macsween A . The reliability and validity of the Astrand nomogram and linear extrapolation for deriving VO2max from submaximal exercise data. J Sports Med Phys Fitness. 2001;41(3):312–7.
27 Fahey TD , Del Valle-Zuris A , Oehlsen G , Trieb M , Seymour J . Pubertal stage differences in hormonal and hematological responses to maximal exercise in males. J Appl Physiol. 1979;46(4):823–7.
28 Armstrong N , Welsman JR . Assessment and interpretation of aerobic fitness in children and adolescents. Exerc Sport Sci Rev. 1994;22(1):435–76. https://doi.org/10.1249/00003677-199401000-00016
29 Butte NF , Puyau MR , Adolph AL , Vohra FA , Zakeri I . Physical activity in nonoverweight and overweight Hispanic children and adolescents. Med Sci Sports Exerc. 2007;39(8):1257–66. https://doi.org/10.1249/mss.0b013e3180621fb6
30 Dencker M , Thorsson O , Karlsson MK , Lindén C , Eiberg S , Wollmer P , et al. Gender differences and determinants of aerobic fitness in children aged 8-11 years. Eur J Appl Physiol. 2007;99(1):19–26. https://doi.org/10.1007/s00421-006-0310-x
31 Zelik KE , Kuo AD . Human walking isn’t all hard work: evidence of soft tissue contributions to energy dissipation and return. J Exp Biol. 2010;213(Pt 24):4257–64. https://doi.org/10.1242/jeb.044297
32 Maggio AB , Hofer MF , Martin XE , Marchand LM , Beghetti M , Farpour-Lambert NJ . Reduced physical activity level and cardiorespiratory fitness in children with chronic diseases. Eur J Pediatr. 2010;169(10):1187–93. https://doi.org/10.1007/s00431-010-1199-2
33 Zanconato S , Baraldi E , Santuz P , Rigon F , Vido L , Da Dalt L , et al. Gas exchange during exercise in obese children. Eur J Pediatr. 1989;148(7):614–7. https://doi.org/10.1007/BF00441512
34 Machado FA , Denadai BS . Validity of maximum heart rate prediction equations for children and adolescents. Arq Bras Cardiol. 2011;97(2):136–40. [Article in English, Portuguese, Spanish] https://doi.org/10.1590/S0066-782X2011005000078
35 Mahon AD , Marjerrison AD , Lee JD , Woodruff ME , Hanna LE . Evaluating the prediction of maximal heart rate in children and adolescents. Res Q Exerc Sport. 2010;81(4):466–71. https://doi.org/10.1080/02701367.2010.10599707
36 Poole DC , Wilkerson DP , Jones AM . Validity of criteria for establishing maximal O2 uptake during ramp exercise tests. Eur J Appl Physiol. 2008;102(4):403–10. https://doi.org/10.1007/s00421-007-0596-3
37 Evans HJ , Ferrar KE , Smith AE , Parfitt G , Eston RG . A systematic review of methods to predict maximal oxygen uptake from submaximal, open circuit spirometry in healthy adults. J Sci Med Sport. 2015;18(2):183–8.
38 Pietrobelli A , Faith MS , Allison DB , Gallagher D , Chiumello G , Heymsfield SB . Body mass index as a measure of adiposity among children and adolescents: a validation study. J Pediatr. 1998;132(2):204–10. https://doi.org/10.1016/S0022-3476(98)70433-0
39 Armstrong N , Williams J , Balding J , Gentle P , Kirby B . The peak oxygen uptake of British children with reference to age, sex and sexual maturity. Eur J Appl Physiol Occup Physiol. 1991;62(5):369–75. https://doi.org/10.1007/BF00634975
40 He Q , Karlberg J . Bmi in childhood and its association with height gain, timing of puberty, and final height. Pediatr Res. 2001;49(2):244–51. https://doi.org/10.1203/00006450-200102000-00019
This study was supported financially by the “Délégation valaisanne de la Loterie Romande”, the “Commission de gestion du fonds cantonal de promotion de la santé” and the Geneva University Hospitals “Contrepoids” Research Funds. The work was independent of the funding.
The authors have no conflicts of interest to declare.